I am pleased to say that the first phase of my Kalman filter coding, namely writing Octave code, is now complete. In doing so I have used/adapted code from the MATLAB toolbox available
here. The second phase of coding, at some future date, will be to convert this code into a C++ .oct function. My code is a stripped down version of the
2D CWPA demo, which models price as a moving object with position and velocity, and which is described in detail with my model assumptions below.
The first thing I had to decide was what to actually model, and I decided on
VWAP. The framework of the Kalman filter is that it tracks an underlying process that is not necessarily directly observable but for which measurements are available. VWAP calculated from OHLC bars fits this framework nicely. If one had access to high frequency daily tick data the VWAP could be calculated exactly, but since the only information available for my purposes is the daily OHLC, the daily OHLC approximation of VWAP is the observable measurement of the "unobservable" exact VWAP.
The next thing I considered was the measurement noise of the filter. Some algebraic manipulation of the VWAP approximation formula (
see here) led me to choose two thirds (or 0.666) of the Hi-Lo range of the bar as the measurement noise associated with any single VWAP approximation, this being the maximum possible range of values that the VWAP can take given a bar's OHLC values.
Finally, for the process noise I employed a simple heuristic of the noise being half the bar to bar variation in successive VWAPs, the other half in this assumption being attributable to the process itself.
Having decided on the above the next step was to initialise the filter covariances, and to do this I decided to use the Median Absolute Deviation (MAD) of the noise processes as a
consistent estimator of the standard deviation and use the scale factor of 1.4826 for normally distributed data (the Kalman filter assumes Gaussian noise) to calculate the noise variances (
see this wiki for more details.) However, I had a concern with "look ahead bias" with this approach but a simple test dispelled these fears. This code box
1279.9 1279.9 1279.9 1279.9 1279.9 1279.9 1279.9 1279.9
1284.4 1284.4 1284.4 1284.4 1284.4 1284.4 1284.4 1284.4
1284.0 1284.0 1284.0 1284.0 1284.0 1284.0 1284.0 1284.0
1283.3 1283.3 1283.3 1283.3 1283.3 1283.3 1283.3 1283.3
1288.2 1288.2 1288.2 1288.2 1288.2 1288.2 1288.2 1288.2
1298.8 1298.7 1298.7 1298.8 1298.7 1298.7 1298.7 1298.7
1305.0 1305.0 1305.0 1305.0 1305.0 1305.0 1305.0 1305.0
1306.1 1306.2 1306.2 1306.1 1306.2 1306.2 1306.2 1306.2
1304.9 1305.0 1305.0 1304.9 1305.0 1305.0 1305.0 1305.0
1308.3 1308.3 1308.3 1308.3 1308.3 1308.3 1308.3 1308.3
1312.0 1312.0 1312.0 1312.0 1312.0 1312.0 1312.0 1312.0
1309.1 1309.1 1309.1 1309.1 1309.1 1309.1 1309.1 1309.1
1304.3 1304.3 1304.3 1304.3 1304.3 1304.3 1304.3 1304.3
1302.3 1302.3 1302.3 1302.3 1302.3 1302.3 1302.3 1302.3
1306.5 1306.5 1306.5 1306.5 1306.4 1306.4 1306.4 1306.4
1314.6 1314.5 1314.5 1314.6 1314.5 1314.5 1314.5 1314.5
1325.1 1325.0 1325.0 1325.1 1325.0 1325.0 1325.0 1325.0
1332.7 1332.7 1332.7 1332.7 1332.7 1332.7 1332.7 1332.7
1336.7 1336.8 1336.8 1336.7 1336.8 1336.8 1336.8 1336.8
1339.7 1339.8 1339.8 1339.7 1339.8 1339.8 1339.8 1339.8
1341.6 1341.7 1341.7 1341.6 1341.7 1341.7 1341.7 1341.7
1338.3 1338.4 1338.4 1338.3 1338.4 1338.4 1338.4 1338.4
1340.6 1340.6 1340.6 1340.6 1340.6 1340.6 1340.6 1340.6
1341.1 1341.1 1341.1 1341.1 1341.1 1341.1 1341.1 1341.1
1340.4 1340.4 1340.4 1340.4 1340.3 1340.3 1340.3 1340.3
1341.3 1341.3 1341.3 1341.3 1341.3 1341.3 1341.3 1341.3
1349.7 1349.7 1349.7 1349.7 1349.6 1349.6 1349.6 1349.6
1357.6 1357.6 1357.6 1357.6 1357.5 1357.5 1357.5 1357.5
1355.2 1355.3 1355.3 1355.2 1355.3 1355.3 1355.3 1355.3
1353.6 1353.6 1353.6 1353.6 1353.6 1353.6 1353.6 1353.6
1356.6 1356.6 1356.6 1356.6 1356.6 1356.6 1356.6 1356.6
1358.2 1358.2 1358.2 1358.2 1358.2 1358.2 1358.2 1358.2
1362.8 1362.7 1362.7 1362.8 1362.7 1362.7 1362.7 1362.7
1362.7 1362.7 1362.7 1362.7 1362.7 1362.7 1362.7 1362.7
1362.6 1362.6 1362.6 1362.6 1362.6 1362.6 1362.6 1362.6
1365.1 1365.1 1365.1 1365.1 1365.1 1365.1 1365.1 1365.1
1360.8 1360.9 1360.9 1360.8 1360.9 1360.9 1360.9 1360.9
1348.8 1348.9 1348.9 1348.8 1348.9 1348.9 1348.9 1348.9
1340.8 1340.8 1340.8 1340.8 1340.8 1340.8 1340.8 1340.8
1349.0 1348.9 1348.9 1349.0 1348.9 1348.9 1348.9 1348.9
1361.7 1361.6 1361.6 1361.7 1361.5 1361.5 1361.5 1361.5
1368.0 1368.0 1368.0 1368.0 1367.9 1367.9 1367.9 1367.9
1379.2 1379.2 1379.2 1379.2 1379.2 1379.2 1379.2 1379.2
1390.3 1390.4 1390.4 1390.3 1390.4 1390.4 1390.4 1390.4
1394.1 1394.2 1394.2 1394.1 1394.2 1394.2 1394.2 1394.2
1397.7 1397.8 1397.8 1397.7 1397.8 1397.8 1397.8 1397.8
1400.6 1400.6 1400.6 1400.6 1400.6 1400.6 1400.6 1400.6
1400.8 1400.8 1400.8 1400.8 1400.8 1400.8 1400.8 1400.8
1399.2 1399.2 1399.2 1399.2 1399.2 1399.2 1399.2 1399.2
1393.2 1393.2 1393.2 1393.2 1393.2 1393.2 1393.2 1393.2
1389.3 1389.3 1389.3 1389.3 1389.3 1389.3 1389.3 1389.3
shows the last 50 values of the Kalman filter with different amounts of data used for the calculations for the initialisation of the filter. The leftmost column shows filter values using all available data for initialisation, the next all data except the most recent 50 values, then all data except the most recent 100 values etc. with the rightmost column being calculated using all data except for the most recent 350 values. This last column is akin to using the data through to the end of 2010, and nothing after this date. Comparison between the left and rightmost columns shows virtually insignificant differences. If one were to begin trading the right hand edge of the chart today, initialisation would be done using all available data. If one then traded for the next one and a half years and then re-initialised the filter using all this "new" data, there would be no practical difference in the filter values over this one and a half year period. So, although there may be "look ahead bias," frankly it doesn't matter. Such is the power of
robust statistics and the recursive calculations of the Kalman filter combined!
This next code box shows my Octave code for the Kalman filter
data = load("-ascii","esmatrix") ;
tick = 0.25 ;
n = length(data(:,4))
finish = input('enter finish, no greater than n ')
if ( finish > length(data(:,4)) )
finish = 0 % i.e. all available data is used
end
open = data(:,4) ;
high = data(:,5) ;
low = data(:,6) ;
close = data(:,7) ;
market_type = data(:,230) ;
clear data
vwap = round( ( ( open .+ close .+ ( (high .+ low) ./ 2 ) ) ./ 3 ) ./ tick) .* tick ;
vwap_process_noise = ( vwap .- shift(vwap,1) ) ./ 2.0 ;
median_vwap_process_noise = median(vwap_process_noise(2:end-finish,1)) ;
vwap_process_noise_deviations = vwap_process_noise(2:end-finish,1) .- median_vwap_process_noise ;
MAD_process_noise = median( abs( vwap_process_noise_deviations ) ) ;
% convert this to variance under the assumption of a normal distribution
std_vwap_noise = 1.4826 * MAD_process_noise ;
process_noise_variance = std_vwap_noise * std_vwap_noise
measurement_noise = 0.666 .* ( high .- low ) ;
median_measurement_noise = median( measurement_noise(1:end-finish,1) ) ;
measurement_noise_deviations = measurement_noise(1:end-finish,1) .- median_measurement_noise ;
MAD_measurement_noise = median( abs( measurement_noise_deviations ) ) ;
% convert this to variance under the assumption of a normal distribution
std_measurement_noise = 1.4826 * MAD_measurement_noise ;
measurement_noise_variance = std_measurement_noise * std_measurement_noise
% Transition matrix for the continous-time system.
F = [0 0 1 0 0 0;
0 0 0 1 0 0;
0 0 0 0 1 0;
0 0 0 0 0 1;
0 0 0 0 0 0;
0 0 0 0 0 0];
% Noise effect matrix for the continous-time system.
L = [0 0;
0 0;
0 0;
0 0;
1 0;
0 1];
% Process noise variance
q = process_noise_variance ;
Qc = diag([q q]);
% Discretisation of the continuous-time system.
[A,Q] = lti_disc(F,L,Qc,1); % last item is dt stepsize set to 1
% Measurement model.
H = [1 0 0 0 0 0;
0 1 0 0 0 0];
% Variance in the measurements.
r1 = measurement_noise_variance ;
R = diag([r1 r1]);
% Initial guesses for the state mean and covariance.
m = [0 vwap(1,1) 0 0 0 0]';
P = diag([0.1 0.1 0.1 0.1 0.5 0.5]) ;
% Space for the estimates.
MM = zeros(size(m,1), length(vwap));
% create vectors for eventual plotting
predict_plot = zeros(length(vwap),1) ;
MM_plot = zeros(length(vwap),1) ;
sigmaP_plus = zeros(length(vwap),1) ;
sigmaP_minus = zeros(length(vwap),1) ;
% Filtering steps.
for ii = 1:length(vwap)
[m,P] = kf_predict(m,P,A,Q);
predict_plot(ii,1) = m(2,1) ;
[m,P] = kf_update(m,P,vwap(ii,:),H,R);
MM(:,ii) = m;
MM_plot(ii,1) = m(2,1) ;
% sigmaP is for storing the current error covariance for plotting purposes
sigmaP = sqrt(diag(P)) ;
sigmaP_plus(ii,1) = MM_plot(ii,1) + 2 * sigmaP(1) ;
sigmaP_minus(ii,1) = MM_plot(ii,1) - 2 * sigmaP(1) ;
end
% output in terminal for checking purposes
kalman_last_50 = [kalman_last_50,MM_plot(end-50:end,1)]
% output for plotting in Gnuplot
x_axis = ( 1:length(vwap) )' ;
A = [x_axis,open,high,low,close,vwap,MM_plot,sigmaP_plus,sigmaP_minus,predict_plot,market_type] ;
dlmwrite('my_cosy_kalman_plot',A)
Note that this code calls three functions; lti_disc, kf_predict and kf_update; which are part of the above mentioned MATLAB toolbox. If readers wish to replicate my results, they will have to download said toolbox and put these functions where they may be called by this script.
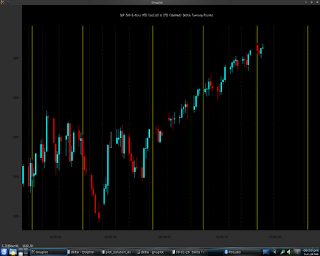
Below is a screen shot of my Kalman filter in action.
This shows the S & P E-mini contact (daily bars) up to a week or so ago. The white line is the Kalman filter, the dotted white lines are the plus and minus 2 sigma levels taken from the covariance matrix and the red and light blue triangles show the output of the kf_predict function, prior to being updated by the kf_update function, but only shown if above (red) or below (blue) the 2 sigma level. As can be seen, while price is obviously trending most points are with these levels. The colour coding of the bars is based upon the market type as determined by
my Naive Bayesian Classifier, Mark 2.
This next screen shot
shows price bars immediately prior to the first screen shot where price is certainly not trending, and it is interesting to note that the kf_predict triangles are now appearing at the turns in price. This fact may mean that the kf_predict function might be a complementary indicator to
my Perfect Oscillator function
and Delta
along with my stable of other turn indicators. The next thing I will have to do is come up with a robust rule set that combines all these disparate indicators into a coherent whole. Also, I am now going to use the Kalman filter output as the input to all my other indicators. Up till now I have been using the typical price; (High+Low+Close)/3; as my input but I think the Kalman filtered VWAP for "today's" price action is a much more meaningful price input than "tomorrow's" pivot point!