In my previous post I said I was trying to develop new indicators from the results of my new PositionBook optimisation routine. In doing so, I need to have a methodology for judging the quality of the indicator(s). In the past I created a Data-Snooping-Tests-GitHub which contains some tests for statistical significance testing and which, of course, can be used on these new indicators. Additionally, for many years I have had a link to tssb on this blog from where a free testing program, VarScreen, and its associated manual are available. Timothy Masters also has a book, Testing and Tuning Market Trading Systems, wherein there is C++ code for an Entropy test, an Octave compiled .oct version of which is shown in the following code box.
#include "octave oct.h"
#include "octave dcolvector.h"
#include "cmath"
#include "algorithm"
DEFUN_DLD ( entropy, args, nargout,
"-*- texinfo -*-\n\
@deftypefn {Function File} {entropy_value =} entropy (@var{input_vector,nbins})\n\
This function takes an input vector and nbins and calculates\n\
the entropy of the input_vector. This input_vector will usually\n\
be an indicator for which we want the entropy value. This value ranges\n\
from 0 to 1 and a minimum value of 0.5 is recommended. Less than 0.1 is\n\
serious and should be addressed. If nbins is not supplied, a default value\n\
of 20 is used. If the input_vector length is < 50, an error will be thrown.\n\
@end deftypefn" )
{
octave_value_list retval_list ;
int nargin = args.length () ;
int nbins , k ;
double entropy , factor , p , sum ;
// check the input arguments
if ( args(0).length () < 50 )
{
error ("Invalid 1st argument length. Input is a vector of length >= 50.") ;
return retval_list ;
}
if ( nargin == 1 )
{
nbins = 20 ;
}
if ( nargin == 2 )
{
nbins = args(1).int_value() ;
}
// end of input checking
ColumnVector input = args(0).column_vector_value () ;
ColumnVector count( nbins ) ;
double max_val = *std::max_element( &input(0), &input( args(0).length () - 1 ) ) ;
double min_val = *std::min_element( &input(0), &input( args(0).length () - 1 ) ) ;
factor = ( nbins - 1.e-10 ) / ( max_val - min_val + 1.e-60 ) ;
for ( octave_idx_type ii ( 0 ) ; ii < args(0).length () ; ii++ ) {
k = ( int ) ( factor * ( input( ii ) - min_val ) ) ;
++count( k ) ; }
sum = 0.0 ;
for ( octave_idx_type ii ( 0 ) ; ii < nbins ; ii++ ) {
if ( count( ii ) ) {
p = ( double ) count( ii ) / args(0).length () ;
sum += p * log ( p ) ; }
}
entropy = -sum / log ( (double) nbins ) ;
retval_list( 0 ) = entropy ;
return retval_list ;
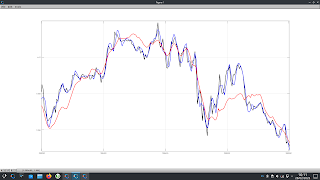
} // end of functionentropy value of 0.7781 and is in fact just random, normally distributed values with a mean of 0 and variance 1. In both plots, the red indicators fail to meet the recommended minimum value, both having entropy values of 0.2314.
It is visually intuitive that in both plots the blue indicators convey more information than the red ones. In creating my new PositionBook indicators I intend to construct them in such a way as to maximise their entropy before I progress to some of the above mentioned tests.