The results of the first set of tests of optimising an indicator via the framework of training a neural net are in, and this post is a presentation of these results and a reflection on this in more general terms. I would encourage readers to look at my previous 2 posts to put this one in context.
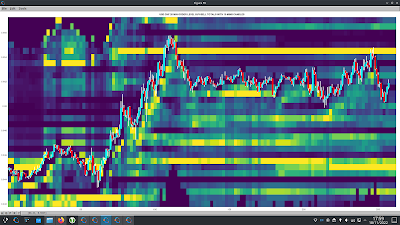
The following chart plot shows 8 weeks of 10 minute price action in the EURUSD forex pair, with the white equity curve being the cumulative sum of open to open tick returns over this period. The green equity curve is a similar cumulative sum of the tick returns based on going long/short when the basic indicator crosses above/below its zero line. Finally, the mass of magenta coloured equity curves are those that result from various simple moving average smoothing, momentum of and smooths of momentum, and short term MACDs of the basic indicator, with the same zero line crossing positioning.
These different magenta equity curves are expressed by setting different weights for the "decision weights" shown in the neural net diagram in the previous 2 posts, e.g. a weight matrix [ 0.25 0.25 0.25 0.25 ] is obviously a 4 bar simple moving, whilst weight matrices [ 0.25 0.25 -0.5 -0.5 ] and [ -0.25 -0.25 0.5 0.5 ] are MACDs of 2 bar fast and 4 bar slow simple moving averages (respectively a fast minus slow MACD and slow minus fast MACD - short term trend following vs. mean reversion?) In this way it is possible to create all the various smooths etc. shown above.
Taking this idea a bit further, it is possible to characterise the more "traditional" way of back testing, i.e. testing over a range of possible indicator look back periods, smooths etc. as an extremely limited or constrained form of neural net training. Consider the neural net diagram of my previous posts - a "traditional" back test is functionally equivalent to:-
- setting the neural net architecture as shown in the above mentioned diagram, but only allowing linear hidden activation units
- not allowing the addition of any bias units
- fixing the input weights and output weights matrices prior to any training and not allowing any updating of these weights to take place
- and only allowing the decision weights to be updated, and limiting this updating to a choice between a limited set of fixed weights and not allowing any error based backpropagation to take place
The next chart plot shows the out of sample result of such limited training. The white and green equity curves are the same as previously described, the cumulative sum of open to open returns and zero line crossings of the basic indicator. The single magenta coloured equity curve is the result of following this limited, "traditional" walk forward optimization
- choose the best set of fixed decision weights over a 2 week window. This best set is decided by choosing the equity curve with the highest Sortino ratio. For the first train/test iteration the 2 week window of training data is not shown but is that data immediately prior to the left hand edge of the plot
- this best set is used out of sample over 1 week of data, the first week of the shown magenta equity curve
- at the end of this first test week, roll the training window forward 1 week so that the new training data consists of the latter week of the first set of training data and the data that has just formed the test week
- repeat the training over this new set of 2 week training data and test out of sample on the immediately following week's data
- keep rolling the window forward, repeating the above, until the end of the test period
The red equity curve is the equity curve that comes from the decision weights that are equivalent to a 3 bar simple moving average of the 1 bar momentum of the basic indicator, shown because this was visually identified in the first post in this series as being "the best." Comparing this equity curve with the magenta ones in the first chart it is obvious that this set of decision weights, out of sample, turns out to be probably the worst of all sets of weights. This is significant because these weights were the ones that were used to initialize the decision weights prior to neural net training.
Finally, the blue equity curve is the out of sample curve for the trained neural net, trained/tested following the same rolling methodology just described above for the magenta curve. In a hand-wavy way, the improvement in performance from the red to the blue equity curves can be said to show the benefits of optimising an indicator's performance via the framework of neural net training. This then begs the question, what if the neural net was initialised with a better set of decision weights, i.e. those of the magenta curve? This will be the subject of my next post.
More in due course.