In the Spring of 2012 and again in the Spring of 2019 I posted a series of posts about the Kalman Filter, which readers can access via the blog archive on the right. In both cases I eventually gave up those particular lines of investigation because of disappointing results. This post is the first in a new series about using the Kalman Filter for sensor fusion, which I had known of before, but due to the paucity of clear information about this online I had never really investigated. However, my recent discovery of this Github and its associated online tutorial has inspired me to a third attempt at using Kalman Filters. What I am going to attempt to do is use the idea of sensor fusion to fuse the output of several functions I have coded in the past, which each extract the dominant cycle from a time series, to hopefully obtain a better representation of the "true underlying cycle."
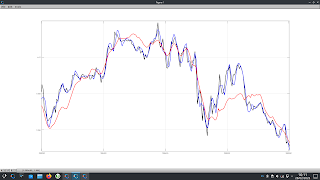
The first step in this process is to determine the measurement noise covariance or, in Kalman Filter terms, the "R" covariance matrix. To do this, I have used the average of two of the outputs from the above mentioned functions to create a new cycle and similarly used two extracted trends (price minus these cycles) averaged to get a new trend. The new cycle and new trend are simply added to each other to create a new price series which is almost identical to the original price series. The screenshot below shows a typical cycle extract,
where the red cycle is the average of the other two extracted cycles, and this following screenshot shows the new trend in red plus the new price alongside the old price (blue and black respectively). Having created a time series thus with known trend and cycle, it is a simple matter to run my cycle extractor functions on this new price, compare the outputs with the known cyclic component of price and calculate the variance of the errors to get the R covariance matrices for 14 different currency crosses.More in due course.

No comments:
Post a Comment