"Trading is statistics and time series analysis." This blog details my progress in developing a systematic trading system for use on the futures and forex markets, with discussion of the various indicators and other inputs used in the creation of the system. Also discussed are some of the issues/problems encountered during this development process. Within the blog posts there are links to other web pages that are/have been useful to me.
Thursday, 27 October 2016
Currency Strength Indicator
In the end I decided to create my own relative currency strength indicator, based on the RSI, by making the length of the indicator adaptive to the measured dominant cycle. The optimal theoretical length for the RSI is half the cycle period, and the price series are smoothed in a [ 1 2 2 1 ] FIR filter prior to the RSI calculations. I used the code in my earlier post to calculate the dominant cycle period, the reason being that since I wrote that post I have watched/listened to a podcast in which John Ehlers recommended using this calculation method for dominant cycle measurement.
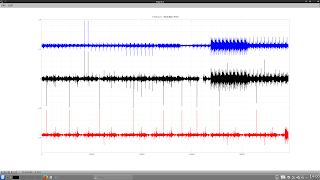
The screenshots below are of the currency strength indicator applied to approx. 200 daily bars of the EURUSD forex pair; first the price chart,
next, the indicator,
and finally an oscillator derived from the two separate currency strength lines.
I think the utility of this indicator is quite obvious from these simple charts. Crossovers of the strength lines ( or equivalently, zero line crossings of the oscillator ) clearly indicate major directional changes, and additionally changes in the slope of the oscillator provide an early warning of impending price direction changes.
I will now start to test this indicator and write about these tests and results in due course.
Friday, 31 July 2020
Currency Strength Candlestick Chart
retval_high_wicks( ii , 6 ) = log( str2double( S.candles{ ii }.mid.h ) / max( str2double( S.candles{ ii }.mid.o ) , str2double( S.candles{ ii }.mid.c ) ) ) ;
retval_low_wicks( ii , 6 ) = log( str2double( S.candles{ ii }.mid.l ) / min( str2double( S.candles{ ii }.mid.o ) , str2double( S.candles{ ii }.mid.c ) ) ) ;[ ii , ~ , v ] = find( [ retval_high_wicks( : , [32 33 34 35 36 37].+5 ) , -1.*retval_low_wicks( : , [5 20 28].+5 ) ] ) ;
new_index_high_wicks( : , 13 ) = accumarray( ii , v , [] , @mean ) ;
[ ii , ~ , v ] = find( [ retval_low_wicks( : , [32 33 34 35 36 37].+5 ) , -1.*retval_high_wicks( : , [5 20 28].+5 ) ] ) ;
new_index_low_wicks( : , 13 ) = accumarray( ii , v , [] , @mean ) ;[32 33 34 35 36 37].+5 and[5 20 28].+5
Wednesday, 3 September 2025
Expressing an Indicator in Neural Net Form
Recently I started investigating relative rotation graphs with a view to perhaps implementing a version of this for use on forex currency pairs. The underlying idea of a relative rotation graph is to plot an asset's relative strength compared to a benchmark and the momentum of this relative strength and to plot this in a form similar to a Polar coordinate system plot, which rotates around a zero point representing zero relative strength and zero relative strength momentum. After some thought it occurred to me that rather than using relative strength against a benchmark I could use the underlying relative strengths of the individual currencies, as calculated by my currency strength indicator, against each other. Furthermore, these underlying log changes in the individual currencies can be normalised using the ideas of brownian motion and then averaged together over different look back periods to create a unique indicator.
indicator_middle_layer = tanh( full_feature_matrix * input_weights ) ;
indicator_nn_output = tanh( indicator_middle_layer * output_weights ) ;
Of course, prior to calling these two lines of code, there is some feature engineering to create the input full_feature_matrix, and the input weights and output_weights matrices taken together are mathematically equivalent to the original indicator calculations. Finally, because this is a neural net expression of the indicator, the non-linear tanh activation function is applied to the hidden middle and output layers of the net.
The following plot shows the original indicator in black and the neural net version of it in blue
over the data shown in this plot of 10 minute bars of the EURUSD forex pair.The red indicator in the plot above is the 1 bar momentum of the neural net indicator plot.
To judge the quality of this indicator I used the entropy measure (measured over 14,000+ 10 minute bars of EURUSD), the results of which are shown next.
entropy_indicator_original = 0.9485
entropy_indicator_nn_output = 0.9933An entropy reading of 0.9933 is probably as good as any trading indicator could hope to achieve (a perfect reading is 1.0) and so the next thing was to quickly back test the indicator performance. Based on the logic of the indicator the obvious long (short) signals are being above (below) the zeroline, or equivalently the sign of the indicator, and for good measure I also tested the sign of the momentum and some simple moving averages thereof.
The following plot shows the equity curves of this quick test where it is visually clear that the blue equity curves are "the best" when plotted in relation to the black "buy and hold" equivalent equity curve. These represent the equity curves of a 3 bar simple moving average of the 1 bar momentum of both the original formulation of the indicator and the neural net implementation. I would point out that these equity curves represent the theoretical equity resulting from trading the London session after 9:00am BST and stopping at 7:00am EST (usually about noon BST) and then starting trading again at 9:00am EST until 17:00pm EST. This schedule avoids the opening sessions (7:00 to 9:00am) in both London and New York because, from my observations of many OHLC charts such as shown above, there are frequently wild swings where price is being pushed to significant points such as volume profile clusters, accumulations of buy/sell orders etc. and in my opinion no indicator can be expected to perform well in that sort of environment. Also avoided are the hours prior to 7:00am BST, i.e. the Asian session or overnight session.
Although these equity curves might not, at first glance, be that impressive, especially as they do not account for trading costs etc. my intent on doing these tests was to determine the configuration of a final "decision" output layer to be added to the neural net implementation of the indicator. A 3 bar simple moving average of the 1 bar momentum implies the necessity to include 4 consecutive readings of the indicator output as input to a final " decision" layer. The following simple, hand-drawn sketch shows what I mean:A discussion of this will be the subject of my next post.Tuesday, 8 November 2016
Preliminary Tests of Currency Strength Indicator
it can be seen that there are a lot of green ( no signal ) bars which, during the randomisation test, can be selected and give equal or greater returns than the signal bars ( blue for longs, red for shorts ). The relative sparsity of the signal bars compared to non-signal bars gives the permutation test, in this instance, low power to detect significance, although I am not able to show that this is actually true in this case.
In the light of the above I decided to conduct a different test, the .m code for which is shown below.
clear all ;
load all_strengths_quad_smooth_21 ;
all_random_entry_distribution_results = zeros( 21 , 3 ) ;
tic();
for ii = 1 : 21
clear -x ii all_strengths_quad_smooth_21 all_random_entry_distribution_results ;
if ii == 1
load audcad_daily_bin_bars ;
mid_price = ( audcad_daily_bars( : , 3 ) .+ audcad_daily_bars( : , 4 ) ) ./ 2 ; mid_price_rets = [ 0 ; diff( mid_price ) ] ;
base_ix = 6 ; term_ix = 7 ;
end
if ii == 2
load audchf_daily_bin_bars ;
mid_price = ( audchf_daily_bars( : , 3 ) .+ audchf_daily_bars( : , 4 ) ) ./ 2 ; mid_price_rets = [ 0 ; diff( mid_price ) ] ;
base_ix = 6 ; term_ix = 4 ;
end
if ii == 3
load audjpy_daily_bin_bars ;
mid_price = ( audjpy_daily_bars( : , 3 ) .+ audjpy_daily_bars( : , 4 ) ) ./ 2 ; mid_price_rets = [ 0 ; diff( mid_price ) ] ;
base_ix = 6 ; term_ix = 5 ;
end
if ii == 4
load audusd_daily_bin_bars ;
mid_price = ( audusd_daily_bars( : , 3 ) .+ audusd_daily_bars( : , 4 ) ) ./ 2 ; mid_price_rets = [ 0 ; diff( mid_price ) ] ;
base_ix = 6 ; term_ix = 1 ;
end
if ii == 5
load cadchf_daily_bin_bars ;
mid_price = ( cadchf_daily_bars( : , 3 ) .+ cadchf_daily_bars( : , 4 ) ) ./ 2 ; mid_price_rets = [ 0 ; diff( mid_price ) ] ;
base_ix = 7 ; term_ix = 4 ;
end
if ii == 6
load cadjpy_daily_bin_bars ;
mid_price = ( cadjpy_daily_bars( : , 3 ) .+ cadjpy_daily_bars( : , 4 ) ) ./ 2 ; mid_price_rets = [ 0 ; diff( mid_price ) ] ;
base_ix = 7 ; term_ix = 5 ;
end
if ii == 7
load chfjpy_daily_bin_bars ;
mid_price = ( chfjpy_daily_bars( : , 3 ) .+ chfjpy_daily_bars( : , 4 ) ) ./ 2 ; mid_price_rets = [ 0 ; diff( mid_price ) ] ;
base_ix = 4 ; term_ix = 5 ;
end
if ii == 8
load euraud_daily_bin_bars ;
mid_price = ( euraud_daily_bars( : , 3 ) .+ euraud_daily_bars( : , 4 ) ) ./ 2 ; mid_price_rets = [ 0 ; diff( mid_price ) ] ;
base_ix = 2 ; term_ix = 6 ;
end
if ii == 9
load eurcad_daily_bin_bars ;
mid_price = ( eurcad_daily_bars( : , 3 ) .+ eurcad_daily_bars( : , 4 ) ) ./ 2 ; mid_price_rets = [ 0 ; diff( mid_price ) ] ;
base_ix = 2 ; term_ix = 7 ;
end
if ii == 10
load eurchf_daily_bin_bars ;
mid_price = ( eurchf_daily_bars( : , 3 ) .+ eurchf_daily_bars( : , 4 ) ) ./ 2 ; mid_price_rets = [ 0 ; diff( mid_price ) ] ;
base_ix = 2 ; term_ix = 4 ;
end
if ii == 11
load eurgbp_daily_bin_bars ;
mid_price = ( eurgbp_daily_bars( : , 3 ) .+ eurgbp_daily_bars( : , 4 ) ) ./ 2 ; mid_price_rets = [ 0 ; diff( mid_price ) ] ;
base_ix = 2 ; term_ix = 3 ;
end
if ii == 12
load eurjpy_daily_bin_bars ;
mid_price = ( eurjpy_daily_bars( : , 3 ) .+ eurjpy_daily_bars( : , 4 ) ) ./ 2 ; mid_price_rets = [ 0 ; diff( mid_price ) ] ;
base_ix = 2 ; term_ix = 5 ;
end
if ii == 13
load eurusd_daily_bin_bars ;
mid_price = ( eurusd_daily_bars( : , 3 ) .+ eurusd_daily_bars( : , 4 ) ) ./ 2 ; mid_price_rets = [ 0 ; diff( mid_price ) ] ;
base_ix = 2 ; term_ix = 1 ;
end
if ii == 14
load gbpaud_daily_bin_bars ;
mid_price = ( gbpaud_daily_bars( : , 3 ) .+ gbpaud_daily_bars( : , 4 ) ) ./ 2 ; mid_price_rets = [ 0 ; diff( mid_price ) ] ;
base_ix = 3 ; term_ix = 6 ;
end
if ii == 15
load gbpcad_daily_bin_bars ;
mid_price = ( gbpcad_daily_bars( : , 3 ) .+ gbpcad_daily_bars( : , 4 ) ) ./ 2 ; mid_price_rets = [ 0 ; diff( mid_price ) ] ;
base_ix = 3 ; term_ix = 7 ;
end
if ii == 16
load gbpchf_daily_bin_bars ;
mid_price = ( gbpchf_daily_bars( : , 3 ) .+ gbpchf_daily_bars( : , 4 ) ) ./ 2 ; mid_price_rets = [ 0 ; diff( mid_price ) ] ;
base_ix = 3 ; term_ix = 4 ;
end
if ii == 17
load gbpjpy_daily_bin_bars ;
mid_price = ( gbpjpy_daily_bars( : , 3 ) .+ gbpjpy_daily_bars( : , 4 ) ) ./ 2 ; mid_price_rets = [ 0 ; diff( mid_price ) ] ;
base_ix = 3 ; term_ix = 5 ;
end
if ii == 18
load gbpusd_daily_bin_bars ;
mid_price = ( gbpusd_daily_bars( : , 3 ) .+ gbpusd_daily_bars( : , 4 ) ) ./ 2 ; mid_price_rets = [ 0 ; diff( mid_price ) ] ;
base_ix = 3 ; term_ix = 1 ;
end
if ii == 19
load usdcad_daily_bin_bars ;
mid_price = ( usdcad_daily_bars( : , 3 ) .+ usdcad_daily_bars( : , 4 ) ) ./ 2 ; mid_price_rets = [ 0 ; diff( mid_price ) ] ;
base_ix = 1 ; term_ix = 7 ;
end
if ii == 20
load usdchf_daily_bin_bars ;
mid_price = ( usdchf_daily_bars( : , 3 ) .+ usdchf_daily_bars( : , 4 ) ) ./ 2 ; mid_price_rets = [ 0 ; diff( mid_price ) ] ;
base_ix = 1 ; term_ix = 4 ;
end
if ii == 21
load usdjpy_daily_bin_bars ;
mid_price = ( usdjpy_daily_bars( : , 3 ) .+ usdjpy_daily_bars( : , 4 ) ) ./ 2 ; mid_price_rets = [ 0 ; diff( mid_price ) ] ;
base_ix = 1 ; term_ix = 5 ;
end
% the returns vectors suitably alligned with position vector
mid_price_rets = shift( mid_price_rets , -1 ) ;
sma2 = sma( mid_price_rets , 2 ) ; sma2_rets = shift( sma2 , -2 ) ; sma3 = sma( mid_price_rets , 3 ) ; sma3_rets = shift( sma3 , -3 ) ;
all_rets = [ mid_price_rets , sma2_rets , sma3_rets ] ;
% delete burn in and 2016 data ( 2016 reserved for out of sample testing )
all_rets( 7547 : end , : ) = [] ; all_rets( 1 : 50 , : ) = [] ;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% simple divergence strategy - be long the uptrending and short the downtrending currency. Uptrends and downtrends determined by crossovers
% of the strengths and their respective smooths
smooth_base = smooth_2_5( all_strengths_quad_smooth_21(:,base_ix) ) ; smooth_term = smooth_2_5( all_strengths_quad_smooth_21(:,term_ix) ) ;
test_matrix = ( all_strengths_quad_smooth_21(:,base_ix) > smooth_base ) .* ( all_strengths_quad_smooth_21(:,term_ix) < smooth_term) ; % +1 for longs
short_vec = ( all_strengths_quad_smooth_21(:,base_ix) < smooth_base ) .* ( all_strengths_quad_smooth_21(:,term_ix) > smooth_term) ; short_vec = find( short_vec ) ;
test_matrix( short_vec ) = -1 ; % -1 for shorts
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% delete burn in and 2016 data
test_matrix( 7547 : end , : ) = [] ; test_matrix( 1 : 50 , : ) = [] ;
[ ix , jx , test_matrix_values ] = find( test_matrix ) ;
no_of_signals = length( test_matrix_values ) ;
% the actual returns performance
real_results = mean( repmat( test_matrix_values , 1 , size( all_rets , 2 ) ) .* all_rets( ix , : ) ) ;
% set up for randomisation test
iters = 5000 ;
imax = size( test_matrix , 1 ) ;
rand_results_distribution_matrix = zeros( iters , size( real_results , 2 ) ) ;
for jj = 1 : iters
rand_idx = randi( imax , no_of_signals , 1 ) ;
rand_results_distribution_matrix( jj , : ) = mean( test_matrix_values .* all_rets( rand_idx , : ) ) ;
endfor
all_random_entry_distribution_results( ii , : ) = ( real_results .- mean( rand_results_distribution_matrix ) ) ./ ...
( 2 .* std( rand_results_distribution_matrix ) ) ;
endfor % end of ii loop
toc()
save -ascii all_random_entry_distribution_results all_random_entry_distribution_results ;
plot(all_random_entry_distribution_results(:,1),'k','linewidth',2,all_random_entry_distribution_results(:,2),'b','linewidth',2,...
all_random_entry_distribution_results(:,3),'r','linewidth',2) ; legend('1 day','2 day','3 day');The first chart shows the results of the unsmoothed currency strength indicator and the second the smoothed version. From this I surmise that the delay introduced by the smoothing is/will be detrimental to performance and so for the nearest future I shall be working on improving the smoothing algorithm used in the indicator calculations.
Sunday, 20 August 2023
Currency Strength Revisited
Recently I responded to a Quantitative Finance forum question here, where I invited the questioner to peruse certain posts on this blog. Apparently the posts do not provide enough information to fully answer the question (my bad) and therefore this post provides what I think will suffice as a full and complete reply, although perhaps not scientifically rigorous.
The original question asked was "Is it possible to separate or decouple the two currencies in a trading pair?" and I believe what I have previously described as a "currency strength indicator" does precisely this (blog search term ---> https://dekalogblog.blogspot.com/search?q=currency+strength+indicator). This post outlines the rationale behind my approach.
Take, for example, the GBPUSD forex pair, and further give it a current (imaginary) value of 1.2500. What does this mean? Of course it means 1 GBP will currently buy you 1.25 USD, or alternatively 1 USD will buy you 1/1.25 = 0.8 GBP. Now rather than write GBPUSD let's express GBPUSD as a ratio thus:- GBP/USD, which expresses the idea of "how many USD are there in a GBP?" in the same way that 9/3 shows how many 3s there are in 9. Now let's imagine at some time period later there is a new pair value, a lower case "gbp/usd" where we can write the relationship
(1) ( GBP / USD ) * ( G / U ) = gbp / usd
to show the change over the time period in question. The ( G / U ) term is a multiplicative term to show the change in value from old GBP/USD 1.2500 to say new value gbp/usd of 1.2600,
e.g. ( G / U ) == ( gbp / usd ) / ( GBP / USD ) == 1.26 / 1.25 == 1.008
from which it is clear that the forex pair has increased by 0.8% in value over this time period. Now, if we imagine that over this time period the underlying, real value of USD has remained unchanged this is equivalent to setting the value U in ( G / U ) to exactly 1, thereby implying that the 0.8% increase in the forex pair value is entirely attributable to a 0.8% increase in the underlying, real value of GBP, i.e. G == 1.008. Alternatively, we can assume that the value of GBP remains unchanged,
e.g. G == 1, which means that U == 1 / 1.008 == 0.9921
which implies that a ( 1 - 0.9921 ) == 0.79% decrease in USD value is responsible for the 0.8% increase in the pair quote.
Of course, given only equation (1) it is impossible to solve for G and U as either can be arbitrarily set to any number greater than zero and then be compensated for by setting the other number such that the constant ( G / U ) will match the required constant to account for the change in the pair value.
However, now let's introduce two other forex pairs (2) and (3) and thus we have:-
(1) ( GBP / USD ) * ( G / U ) = gbp / usd
(2) ( EUR / USD ) * ( E / U ) = eur / usd
(3) ( EUR / GBP ) * ( E / G ) = eur / gbp
We now have three equations and three unknowns, namely G, E and U, and so this system of equations could be laboriously, mathematically solved by substitution.
However, in my currency strength indicator I have taken a different approach. Instead of solving mathematically I have written an error function which takes as arguments a list of G, E, U, ... etc. for all currency multipliers relevant to all the forex quotes I have access to, approximately 47 various crosses which themselves are inputs to the error function, and this function is supplied to Octave's fminunc function to simultaneously solve for all G, E, U, ... etc. given all forex market quotes. The initial starting values for all G, E, U, ... etc. are 1, implying no change in values across the market. These starting values consistently converge to the same final values for G, E, U, ... etc for each separate period's optimisation iterations.
Having got all G, E, U, ... etc. what can be done? Well, taking G for example, we can write
(4) GBP * G = gbp
for the underlying, real change in the value of GBP. Dividing each side of (4) by GBP and taking logs we get
(5) log( G ) = log( gbp / GBP )
i.e. the log of the fminunc returned value for the multiplicative constant G is the equivalent of the log return of GBP independent of all other currencies, or as the original forum question asked, the (change in) value of GBP separated or decoupled the from the pair in which it is quoted.
Of course, having the individual log returns of separated or decoupled currencies, there are many things that can be done with them, such as:-
- create indices for each currency
- apply technical analysis to these separate indices
- intermarket currency analysis
- input to machine learning (ML) models
- possibly create new and unique currency indicators
Examples of the creation of "alternative price charts" and indices are shown below
where the black line is the actual 10 minute closing prices of GBPUSD over the last week (13th to 18th August) with the corresponding GBP price (blue line) being the "alternative" GBPUSD chart if U is held at 1 in the ( G / U ) term and G allowed to be its derived, optimised value, and the USD price (red line) being the alternative chart if G is held at 1 and U allowed to be its derived, optimised value.
This second chart shows a more "traditional" index like chart
where the starting values are 1 and both the G and U values take their derived values. As can be seen, over the week there was upwards momentum in both the GBP and USD, with the greater momentum being in the GBP resulting in a higher GBPUSD quote at the end of the week. If, in the second chart the blue GBP line had been flat at a value of 1 all week, the upwards momentum in USD would have resulted in a lower week ending quoted value of GBPUSD, as seen in the red USD line in the first chart. Having access to these real, decoupled returns allows one to see through the given, quoted forex prices in the manner of viewing the market as though through X-ray vision.I hope readers find this post enlightening, and if you find some other uses for this idea, I would be interested in hearing how you use it.
Monday, 28 May 2018
An Improved Currency Strength Indicator plus Gold and Silver Indices?
The motivation for this came about from looking at chart plots such as this,
which shows Gold prices in the first row, Silver in the second and a selection of forex cross rates in the third and final row. The charts are on a daily time scale and show prices since the beginning of 2018 up to and including 25th May, data from Oanda.
If one looks at the price of gold and asks oneself if the price is moving up or down, the answer will depend on which gold price currency denomination chart one looks at. In the latter part of the charts ( from about time ix 70 onwards ) the gold price goes up in pounds Sterling and Euro and down in US dollars. Obviously, by looking at the relevant exchange rates in the third row, a large part of this gold price movement is due to changes in the strength of the underlying currencies. Therefore, the problem to be addressed is that movements in the price of gold are confounded with movements in the price of the currencies, and it would be ideal if the gold price movement could be separated out from the currency movements, which would then allow for the currency strengths to also be determined.
One approach I have been toying with is to postulate a simple, geometric change model whereby the price of gold is multiplied by a constant, let's call it x_g, for example x_g = 1.01 represents a 1% increase in the "intrinsic" value of gold, and then adjust the obtained value of this multiplication to take in to account the change in the value of the currency. The code box below expresses this idea, in somewhat clunky Octave code.
% xau_gbp using gbp_usd
new_val_gold_in_old_currency_value = current_data(1,1) * x_g ;
new_val_gold_in_new_currency_value = new_val_gold_in_old_currency_value * exp( -log( current_data(2,6) / current_data(1,6) ) ) ;
mse_vector(1) = log( current_data(2,1) / new_val_gold_in_new_currency_value )^2 ;
% xau_usd using gbp_usd
new_val_gold_in_old_currency_value = current_data(1,2) * x_g ;
new_val_gold_in_new_currency_value = new_val_gold_in_old_currency_value * exp( log( current_data(2,6) / current_data(1,6) ) ) ;
mse_vector(2) = log( current_data(2,2) / new_val_gold_in_new_currency_value )^2 ; The above would be repeated for all gold price currency denominations and the relevant forex pairs and be part of a function, for x_g, which is to be minimised by the Octave fminunc function. Observant readers might note that the error to be minimised is the square of the log of the accuracy ratio. Interested readers are referred to the paper A Better Measure of Relative Prediction Accuracy for Model Selection and Model Estimation for an explanation of this and why it is a suitable error metric for a geometric model.
The chart below is a repeat of the one above, with the addition of a gold index, a silver index and currency strengths indices calculated from a preliminary subset of all gold price currency denominations using the above methodology.
In the first two rows, the blue lines are the calculated gold and silver indices, all normalised to start at the first price at the far left of each respective currency denomination. The silver index was calculated using the relationship between the gold x_g value and the xau xag ratio. Readers will see that these indices are similarly invariant to the currency in which they are expressed ( the geometric bar to bar changes in the indices are identical ) but each is highly correlated to its underlying currency. They could be calculated from an arbitrary index starting point, such as 100, and therefore can be considered to be an index of the changes in the intrinsic value of gold.
When it comes to currency strengths most indicators I have come across are variations of a single theme, namely: averages of all the changes for a given set of forex pairs, whether these changes be expressed as logs, percentages, values or whatever. Now that we have an absolute, intrinsic value gold index, it is a simple matter to parse out the change in the currency from the change in the gold price in this currency.
The third row of the second chart above shows these currency strengths for the two base currencies plotted - GBP and EUR - again normalised to the first charted price on the left. Although in this chart only observable for the Euro, it can be seen that the index again is invariant, similar to gold and silver above. Perhaps more interestingly, the red line is a cumulative product of the ratio of base currency index change to the term currency index change, normalised as described above. It can be seen that the red line almost exactly overwrites the underlying black line, which is the actual cross rate plot. This red line is plotted as a sanity check and it is gratifying to see such an accurate overwrite.
I think this idea shows great promise and for the nearest future I shall be working to extend it beyond the preliminary data set used above. More in due course.
Thursday, 20 April 2017
Using the BayesOpt Library to Optimise my Planned Neural Net
My intent was to design a Nonlinear autoregressive exogenous model using my currency strength indicator as the main exogenous input, along with other features derived from the use of Savitzky-Golay filter convolution to model velocity, acceleration etc. I decided that rather than model prices directly, I would model the 20 period simple moving average because it would seem reasonable to assume that modelling a smooth function would be easier, and from this average it is a trivial matter to reverse engineer to get to the underlying price.
Given that my projected feature space/lookback length/number of nodes combination is/was a triple digit, discrete dimensional problem, I used the "bayesoptdisc" function from the BayesOpt library to perform a discrete Bayesian optimisation over these parameters, the main Octave script for this being shown below.
clear all ;
% load the data
% load eurusd_daily_bin_bars ;
% load gbpusd_daily_bin_bars ;
% load usdchf_daily_bin_bars ;
load usdjpy_daily_bin_bars ;
load all_rel_strengths_non_smooth ;
% all_rel_strengths_non_smooth = [ usd_rel_strength_non_smooth eur_rel_strength_non_smooth gbp_rel_strength_non_smooth chf_rel_strength_non_smooth ...
% jpy_rel_strength_non_smooth aud_rel_strength_non_smooth cad_rel_strength_non_smooth ] ;
% extract relevant data
% price = ( eurusd_daily_bars( : , 3 ) .+ eurusd_daily_bars( : , 4 ) ) ./ 2 ; % midprice
% price = ( gbpusd_daily_bars( : , 3 ) .+ gbpusd_daily_bars( : , 4 ) ) ./ 2 ; % midprice
% price = ( usdchf_daily_bars( : , 3 ) .+ usdchf_daily_bars( : , 4 ) ) ./ 2 ; % midprice
price = ( usdjpy_daily_bars( : , 3 ) .+ usdjpy_daily_bars( : , 4 ) ) ./ 2 ; % midprice
base_strength = all_rel_strengths_non_smooth( : , 1 ) .- 0.5 ;
term_strength = all_rel_strengths_non_smooth( : , 5 ) .- 0.5 ;
% clear unwanted data
% clear eurusd_daily_bars all_rel_strengths_non_smooth ;
% clear gbpusd_daily_bars all_rel_strengths_non_smooth ;
% clear usdchf_daily_bars all_rel_strengths_non_smooth ;
clear usdjpy_daily_bars all_rel_strengths_non_smooth ;
global start_opt_line_no = 200 ;
global stop_opt_line_no = 7545 ;
% get matrix coeffs
slope_coeffs = generalised_sgolay_filter_coeffs( 5 , 2 , 1 ) ;
accel_coeffs = generalised_sgolay_filter_coeffs( 5 , 2 , 2 ) ;
jerk_coeffs = generalised_sgolay_filter_coeffs( 5 , 3 , 3 ) ;
% create features
sma20 = sma( price , 20 ) ;
global targets = sma20 ;
[ sma_max , sma_min ] = adjustable_lookback_max_min( sma20 , 20 ) ;
global sma20r = zeros( size(sma20,1) , 5 ) ;
global sma20slope = zeros( size(sma20,1) , 5 ) ;
global sma20accel = zeros( size(sma20,1) , 5 ) ;
global sma20jerk = zeros( size(sma20,1) , 5 ) ;
global sma20diffs = zeros( size(sma20,1) , 5 ) ;
global sma20diffslope = zeros( size(sma20,1) , 5 ) ;
global sma20diffaccel = zeros( size(sma20,1) , 5 ) ;
global sma20diffjerk = zeros( size(sma20,1) , 5 ) ;
global base_strength_f = zeros( size(sma20,1) , 5 ) ;
global term_strength_f = zeros( size(sma20,1) , 5 ) ;
base_term_osc = base_strength .- term_strength ;
global base_term_osc_f = zeros( size(sma20,1) , 5 ) ;
slope_bt_osc = rolling_endpoint_gen_poly_output( base_term_osc , 5 , 2 , 1 ) ; % no_of_points(p),filter_order(n),derivative(s)
global slope_bt_osc_f = zeros( size(sma20,1) , 5 ) ;
accel_bt_osc = rolling_endpoint_gen_poly_output( base_term_osc , 5 , 2 , 2 ) ; % no_of_points(p),filter_order(n),derivative(s)
global accel_bt_osc_f = zeros( size(sma20,1) , 5 ) ;
jerk_bt_osc = rolling_endpoint_gen_poly_output( base_term_osc , 5 , 3 , 3 ) ; % no_of_points(p),filter_order(n),derivative(s)
global jerk_bt_osc_f = zeros( size(sma20,1) , 5 ) ;
slope_base_strength = rolling_endpoint_gen_poly_output( base_strength , 5 , 2 , 1 ) ; % no_of_points(p),filter_order(n),derivative(s)
global slope_base_strength_f = zeros( size(sma20,1) , 5 ) ;
accel_base_strength = rolling_endpoint_gen_poly_output( base_strength , 5 , 2 , 2 ) ; % no_of_points(p),filter_order(n),derivative(s)
global accel_base_strength_f = zeros( size(sma20,1) , 5 ) ;
jerk_base_strength = rolling_endpoint_gen_poly_output( base_strength , 5 , 3 , 3 ) ; % no_of_points(p),filter_order(n),derivative(s)
global jerk_base_strength_f = zeros( size(sma20,1) , 5 ) ;
slope_term_strength = rolling_endpoint_gen_poly_output( term_strength , 5 , 2 , 1 ) ; % no_of_points(p),filter_order(n),derivative(s)
global slope_term_strength_f = zeros( size(sma20,1) , 5 ) ;
accel_term_strength = rolling_endpoint_gen_poly_output( term_strength , 5 , 2 , 2 ) ; % no_of_points(p),filter_order(n),derivative(s)
global accel_term_strength_f = zeros( size(sma20,1) , 5 ) ;
jerk_term_strength = rolling_endpoint_gen_poly_output( term_strength , 5 , 3 , 3 ) ; % no_of_points(p),filter_order(n),derivative(s)
global jerk_term_strength_f = zeros( size(sma20,1) , 5 ) ;
min_max_range = sma_max .- sma_min ;
for ii = 51 : size( sma20 , 1 ) - 1 % one step ahead is target
targets(ii) = 2 * ( ( sma20(ii+1) - sma_min(ii) ) / min_max_range(ii) - 0.5 ) ;
% scaled sma20
sma20r(ii,:) = 2 .* ( ( flipud( sma20(ii-4:ii,1) )' .- sma_min(ii) ) ./ min_max_range(ii) .- 0.5 ) ;
sma20slope(ii,:) = fliplr( ( 2 .* ( ( sma20(ii-4:ii,1)' .- sma_min(ii) ) ./ min_max_range(ii) .- 0.5 ) ) * slope_coeffs ) ;
sma20accel(ii,:) = fliplr( ( 2 .* ( ( sma20(ii-4:ii,1)' .- sma_min(ii) ) ./ min_max_range(ii) .- 0.5 ) ) * accel_coeffs ) ;
sma20jerk(ii,:) = fliplr( ( 2 .* ( ( sma20(ii-4:ii,1)' .- sma_min(ii) ) ./ min_max_range(ii) .- 0.5 ) ) * jerk_coeffs ) ;
% scaled diffs of sma20
sma20diffs(ii,:) = fliplr( diff( 2.* ( ( sma20(ii-5:ii,1) .- sma_min(ii) ) ./ min_max_range(ii) .- 0.5 ) )' ) ;
sma20diffslope(ii,:) = fliplr( diff( 2.* ( ( sma20(ii-5:ii,1) .- sma_min(ii) ) ./ min_max_range(ii) .- 0.5 ) )' * slope_coeffs ) ;
sma20diffaccel(ii,:) = fliplr( diff( 2.* ( ( sma20(ii-5:ii,1) .- sma_min(ii) ) ./ min_max_range(ii) .- 0.5 ) )' * accel_coeffs ) ;
sma20diffjerk(ii,:) = fliplr( diff( 2.* ( ( sma20(ii-5:ii,1) .- sma_min(ii) ) ./ min_max_range(ii) .- 0.5 ) )' * jerk_coeffs ) ;
% base strength
base_strength_f(ii,:) = fliplr( base_strength(ii-4:ii)' ) ;
slope_base_strength_f(ii,:) = fliplr( slope_base_strength(ii-4:ii)' ) ;
accel_base_strength_f(ii,:) = fliplr( accel_base_strength(ii-4:ii)' ) ;
jerk_base_strength_f(ii,:) = fliplr( jerk_base_strength(ii-4:ii)' ) ;
% term strength
term_strength_f(ii,:) = fliplr( term_strength(ii-4:ii)' ) ;
slope_term_strength_f(ii,:) = fliplr( slope_term_strength(ii-4:ii)' ) ;
accel_term_strength_f(ii,:) = fliplr( accel_term_strength(ii-4:ii)' ) ;
jerk_term_strength_f(ii,:) = fliplr( jerk_term_strength(ii-4:ii)' ) ;
% base term oscillator
base_term_osc_f(ii,:) = fliplr( base_term_osc(ii-4:ii)' ) ;
slope_bt_osc_f(ii,:) = fliplr( slope_bt_osc(ii-4:ii)' ) ;
accel_bt_osc_f(ii,:) = fliplr( accel_bt_osc(ii-4:ii)' ) ;
jerk_bt_osc_f(ii,:) = fliplr( jerk_bt_osc(ii-4:ii)' ) ;
endfor
% create xset for bayes routine
% raw indicator
xset = zeros( 4 , 5 ) ; xset( 1 , : ) = 1 : 5 ;
% add the slopes
to_add = zeros( 4 , 15 ) ;
to_add( 1 , : ) = [ 1 2 2 3 3 3 4 4 4 4 5 5 5 5 5 ] ;
to_add( 2 , : ) = [ 1 1 2 1 2 3 1 2 3 4 1 2 3 4 5 ] ;
xset = [ xset to_add ] ;
% add accels
to_add = zeros( 4 , 21 ) ;
to_add( 1 , : ) = [ 1 2 2 2 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4 ] ;
to_add( 2 , : ) = [ 1 1 2 2 1 2 2 3 3 3 1 2 3 4 2 3 3 4 4 4 4 ] ;
to_add( 3 , : ) = [ 1 1 1 2 1 1 2 1 2 3 1 1 1 1 2 2 3 1 2 3 4 ] ;
xset = [ xset to_add ] ;
% add jerks
to_add = zeros( 4 , 70 ) ;
to_add( 1 , : ) = [ 1 2 2 2 2 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 ] ;
to_add( 2 , : ) = [ 1 1 2 2 2 1 2 2 2 3 3 3 3 3 3 1 2 2 2 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 1 2 2 2 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 ] ;
to_add( 3 , : ) = [ 1 1 1 2 2 1 1 2 2 1 2 2 3 3 3 1 1 2 2 1 2 2 3 3 3 1 2 2 3 3 3 4 4 4 4 1 1 2 2 1 2 2 3 3 3 1 2 2 3 3 3 4 4 4 4 1 2 2 3 3 3 4 4 4 4 5 5 5 5 5 ] ;
to_add( 4 , : ) = [ 1 1 1 1 2 1 1 1 2 1 1 2 1 2 3 1 1 1 2 1 1 2 1 2 3 1 1 2 1 2 3 1 2 3 4 1 1 1 2 1 1 2 1 2 3 1 1 2 1 2 3 1 2 3 4 1 1 2 1 2 3 1 2 3 4 1 2 3 4 5 ] ;
xset = [ xset to_add ] ;
% construct all_xset for combinations of indicators and look back lengths
all_zeros = zeros( size( xset ) ) ;
all_xset = [ xset ; repmat( all_zeros , 3 , 1 ) ] ;
all_xset = [ all_xset [ xset ; xset ; all_zeros ; all_zeros ] ] ;
all_xset = [ all_xset [ xset ; all_zeros ; xset ; all_zeros ] ] ;
all_xset = [ all_xset [ xset ; all_zeros ; all_zeros ; xset ] ] ;
all_xset = [ all_xset [ xset ; xset ; xset ; all_zeros ] ] ;
all_xset = [ all_xset [ xset ; xset ; all_zeros ; xset ] ] ;
all_xset = [ all_xset [ xset ; all_zeros ; xset ; xset ] ] ;
all_xset = [ all_xset repmat( xset , 4 , 1 ) ] ;
ones_all_xset = ones( 1 , size( all_xset , 2 ) ) ;
% now add layer for number of neurons and extend as necessary
max_number_of_neurons_in_layer = 20 ;
parameter_matrix = [] ;
for ii = 2 : max_number_of_neurons_in_layer % min no. of neurons is 2, max = max_number_of_neurons_in_layer
parameter_matrix = [ parameter_matrix [ ii .* ones_all_xset ; all_xset ] ] ;
endfor
% now the actual bayes optimisation routine
% set the parameters
params.n_iterations = 190; % bayesopt library default is 190
params.n_init_samples = 10;
params.crit_name = 'cEIa'; % cEI is default. cEIa is an annealed version
params.surr_name = 'sStudentTProcessNIG';
params.noise = 1e-6;
params.kernel_name = 'kMaternARD5';
params.kernel_hp_mean = [1];
params.kernel_hp_std = [10];
params.verbose_level = 1; % 3 to path below
params.log_filename = '/home/dekalog/Documents/octave/cplusplus.oct_functions/nn_functions/optimise_narx_ind_lookback_nodes_log';
params.l_type = 'L_MCMC' ; % L_EMPIRICAL is default
params.epsilon = 0.5 ; % probability of performing a random (blind) evaluation of the target function.
% Higher values implies forced exploration while lower values relies more on the exploration/exploitation policy of the criterion. 0 is default
% the function to optimise
fun = 'optimise_narx_ind_lookback_nodes_rolling' ;
% the call to the Bayesopt library function
bayesoptdisc( fun , parameter_matrix , params ) ;
% result is the minimum as a vector (x_out) and the value of the function at the minimum (y_out)- load all the relevant data ( in this case a forex pair )
- creates a set of scaled features
- creates a necessary parameter matrix for the discrete optimisation function
- sets the parameters for the optimisation routine
- and finally calls the "bayesoptdisc" function
The actual function to be optimised is given in the following code box, and is basically a looped neural net training routine.
## Copyright (C) 2017 dekalog
##
## This program is free software; you can redistribute it and/or modify it
## under the terms of the GNU General Public License as published by
## the Free Software Foundation; either version 3 of the License, or
## (at your option) any later version.
##
## This program is distributed in the hope that it will be useful,
## but WITHOUT ANY WARRANTY; without even the implied warranty of
## MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
## GNU General Public License for more details.
##
## You should have received a copy of the GNU General Public License
## along with this program. If not, see .
## -*- texinfo -*-
## @deftypefn {} {@var{retval} =} optimise_narx_ind_lookback_nodes_rolling (@var{input1})
##
## @seealso{}
## @end deftypefn
## Author: dekalog
## Created: 2017-03-21
function [ retval ] = optimise_narx_ind_lookback_nodes_rolling( input1 )
% declare all the global variables so the function can "see" them
global start_opt_line_no ;
global stop_opt_line_no ;
global targets ;
global sma20r ; % 2
global sma20slope ;
global sma20accel ;
global sma20jerk ;
global sma20diffs ;
global sma20diffslope ;
global sma20diffaccel ;
global sma20diffjerk ;
global base_strength_f ;
global slope_base_strength_f ;
global accel_base_strength_f ;
global jerk_base_strength_f ;
global term_strength_f ;
global slope_term_strength_f ;
global accel_term_strength_f ;
global jerk_term_strength_f ;
global base_term_osc_f ;
global slope_bt_osc_f ;
global accel_bt_osc_f ;
global jerk_bt_osc_f ;
% build feature matrix from the above global variable according to parameters in input1
hidden_layer_size = input1(1) ;
% training targets
Y = targets( start_opt_line_no:stop_opt_line_no , 1 ) ;
% create empty feature matrix
X = [] ;
% which will always have at least one element of the main price series for the NARX
X = [ X sma20r( start_opt_line_no:stop_opt_line_no , 1:input1(2) ) ] ;
% go through input1 values in turn and add to X if necessary
if input1(3) > 0
X = [ X sma20slope( start_opt_line_no:stop_opt_line_no , 1:input1(3) ) ] ;
endif
if input1(4) > 0
X = [ X sma20accel( start_opt_line_no:stop_opt_line_no , 1:input1(4) ) ] ;
endif
if input1(5) > 0
X = [ X sma20jerk( start_opt_line_no:stop_opt_line_no , 1:input1(5) ) ] ;
endif
if input1(6) > 0
X = [ X sma20diffs( start_opt_line_no:stop_opt_line_no , 1:input1(6) ) ] ;
endif
if input1(7) > 0
X = [ X sma20diffslope( start_opt_line_no:stop_opt_line_no , 1:input1(7) ) ] ;
endif
if input1(8) > 0
X = [ X sma20diffaccel( start_opt_line_no:stop_opt_line_no , 1:input1(8) ) ] ;
endif
if input1(9) > 0
X = [ X sma20diffjerk( start_opt_line_no:stop_opt_line_no , 1:input1(9) ) ] ;
endif
if input1(10) > 0 % input for base and term strengths together
X = [ X base_strength_f( start_opt_line_no:stop_opt_line_no , 1:input1(10) ) ] ;
X = [ X term_strength_f( start_opt_line_no:stop_opt_line_no , 1:input1(10) ) ] ;
endif
if input1(11) > 0
X = [ X slope_base_strength_f( start_opt_line_no:stop_opt_line_no , 1:input1(11) ) ] ;
X = [ X slope_term_strength_f( start_opt_line_no:stop_opt_line_no , 1:input1(11) ) ] ;
endif
if input1(12) > 0
X = [ X accel_base_strength_f( start_opt_line_no:stop_opt_line_no , 1:input1(12) ) ] ;
X = [ X accel_term_strength_f( start_opt_line_no:stop_opt_line_no , 1:input1(12) ) ] ;
endif
if input1(13) > 0
X = [ X jerk_base_strength_f( start_opt_line_no:stop_opt_line_no , 1:input1(13) ) ] ;
X = [ X jerk_term_strength_f( start_opt_line_no:stop_opt_line_no , 1:input1(13) ) ] ;
endif
if input1(14) > 0
X = [ X base_term_osc_f( start_opt_line_no:stop_opt_line_no , 1:input1(14) ) ] ;
endif
if input1(15) > 0
X = [ X slope_bt_osc_f( start_opt_line_no:stop_opt_line_no , 1:input1(15) ) ] ;
endif
if input1(16) > 0
X = [ X accel_bt_osc_f( start_opt_line_no:stop_opt_line_no , 1:input1(16) ) ] ;
endif
if input1(17) > 0
X = [ X jerk_bt_osc_f( start_opt_line_no:stop_opt_line_no , 1:input1(17) ) ] ;
endif
% now the X features matrix has been formed, get its size
X_rows = size( X , 1 ) ; X_cols = size( X , 2 ) ;
X = [ ones( X_rows , 1 ) X ] ; % add bias unit to X
fan_in = X_cols + 1 ; % no. of inputs to a node/unit, including bias
fan_out = 1 ; % no. of outputs from node/unit
r = sqrt( 6 / ( fan_in + fan_out ) ) ;
rolling_window_length = 100 ;
n_iters = 100 ;
n_iter_errors = zeros( n_iters , 1 ) ;
all_errors = zeros( X_rows - ( rolling_window_length - 1 ) - 1 , 1 ) ;
rolling_window_loop_iter = 0 ;
for rolling_window_loop = rolling_window_length : X_rows - 1
rolling_window_loop_iter = rolling_window_loop_iter + 1 ;
% train n_iters no. of nets and put the error stats in n_iter_errors
for ii = 1 : n_iters
% initialise weights
% see https://stats.stackexchange.com/questions/47590/what-are-good-initial-weights-in-a-neural-network
% One option is Orthogonal random matrix initialization for input_to_hidden weights
% w_i = rand( X_cols + 1 , hidden_layer_size ) ;
% [ u , s , v ] = svd( w_i ) ;
% input_to_hidden = [ ones( X_rows , 1 ) X ] * u ; % adding bias unit to X
% using fan_in and fan_out for tanh
w_i = ( rand( X_cols + 1 , hidden_layer_size ) .* ( 2 * r ) ) .- r ;
input_to_hidden = X( rolling_window_loop - ( rolling_window_length - 1 ) : rolling_window_loop , : ) * w_i ;
% push the input_to_hidden through the chosen sigmoid function
hidden_layer_output = sigmoid_lecun_m( input_to_hidden ) ;
% add bias unit for the output from hidden
hidden_layer_output = [ ones( rolling_window_length , 1 ) hidden_layer_output ] ;
% use hidden_layer_output as the input to a linear regression fit to targets Y
% a la Extreme Learning Machine
% w = ( inv( X' * X ) * X' ) * y ; the "classic" way for linear regression, where
% X = hidden_layer_output, but
w = ( ( hidden_layer_output' * hidden_layer_output ) \ hidden_layer_output' ) * Y( rolling_window_loop - ( rolling_window_length - 1 ) : rolling_window_loop , 1 ) ;
% is quicker and recommended
% use these current values of w_i and w for out of sample test
os_input_to_hidden = X( rolling_window_loop + 1 , : ) * w_i ;
os_hidden_layer_output = sigmoid_lecun_m( os_input_to_hidden ) ;
os_hidden_layer_output = [ 1 os_hidden_layer_output ] ; % add bias
os_output = os_hidden_layer_output * w ;
n_iter_errors( n_iters ) = abs( Y( rolling_window_loop + 1 , 1 ) - os_output ) ;
endfor
all_errors( rolling_window_loop_iter ) = mean( n_iter_errors ) ;
endfor % rolling_window_loop
retval = mean( all_errors ) ;
clear X w_i ;
endfunction
The results of running the above are quite interesting. The first surprise is that the currency strength indicator and features derived from it were not included in the optimal model for any of the four tested pairs. Secondly, for all pairs, a scaled version of a 20 bar price momentum function, and derived features, was included in the optimal model. Finally, again for all pairs, there was a symmetrically decreasing lookback period across the selected features, and when averaged across all pairs the following pattern results: 10 3 3 2 1 3 3 2 1, which is to be read as:
- 10 nodes (plus a bias node) in the hidden layer
- lookback length of 3 for the scaled values of the SMA20 and the 20 bar scaled momentum function
- lookback length of 3 for the slopes/rates of change of the above
- lookback length of 2 for the "accelerations" of the above
- lookback length of 1 for the "jerks" of the above
Thursday, 11 October 2018
"Black Swan" Data Cleaning
The chart itself is a plot of log returns of various forex crosses and Gold and Silver log returns, concatenated into one long vector. The black is the actual return of the underlying, the blue is the return of the base currency and the red is the cross currency, both of these being calculated from indices formed from the currency strength indicator.
By looking at the dates these spikes occur and then checking online I have flagged four historical "Black swan" events that occured within the time frame the data covers, which are listed in chronological order below:
- Precious metals price collapse in mid April 2013
- Swiss Franc coming off its peg to the Euro in January 2015
- Fears over the Hong Kong dollar and Renminbi currency peg in January 2016
- Brexit black Friday
It can be seen that the final chart shows much more homogeneous data within each concatenated series, which should have benefits when said data is used as machine learning input. Also, the data that has been deleted will provide a useful, extreme test set to stress test any finished model. More in due course.
Saturday, 6 June 2020
Downloading FX Pairs via Oanda API to Calculate Currency Strength Indicator
## Copyright (C) 2020 dekalog
##
## This program is free software: you can redistribute it and/or modify it
## under the terms of the GNU General Public License as published by
## the Free Software Foundation, either version 3 of the License, or
## (at your option) any later version.
##
## This program is distributed in the hope that it will be useful, but
## WITHOUT ANY WARRANTY; without even the implied warranty of
## MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
## GNU General Public License for more details.
##
## You should have received a copy of the GNU General Public License
## along with this program. If not, see
## .
## -*- texinfo -*-
## @deftypefn {} {@var{retval} =} get_currency_index_10m_pairs()
##
## This function gets the date and time value of the last currency index update for
## 10 minute bars by reading the last line of the file at:
##
## "/home/path/to/file"
##
## and then downloads all the currencies required to calculate new values for
## new currency index calculations, via looped Oanda API calls.
##
##The RETVAL is a matrix of GMT dates in the form
## YYYY:MM:DD:HH:MM in the first 5 columns, followed by the 45 required
## currency candlestick close values.
##
## @seealso{}
## @end deftypefn
## Author: dekalog
## Created: 2020-06-01
function retval = get_currency_index_10m_pairs()
## cell array of currency crosses to iterrate over to get the complete set
## of currency crosses to create a currency index
iter_vec = {'AUD_CAD','AUD_CHF','AUD_HKD','AUD_JPY','AUD_NZD','AUD_SGD',...
'AUD_USD','CAD_CHF','CAD_HKD','CAD_JPY','CAD_SGD','CHF_HKD','CHF_JPY',...
'EUR_AUD','EUR_CAD','EUR_CHF','EUR_GBP','EUR_HKD','EUR_JPY','EUR_NZD',...
'EUR_SGD','EUR_USD','GBP_AUD','GBP_CAD','GBP_CHF','GBP_HKD','GBP_JPY',...
'GBP_NZD','GBP_SGD','GBP_USD','HKD_JPY','NZD_CAD','NZD_CHF','NZD_HKD',...
'NZD_JPY','NZD_SGD','NZD_USD','SGD_CHF','SGD_HKD','SGD_JPY','USD_CAD',...
'USD_CHF','USD_HKD','USD_JPY','USD_SGD'} ;
## read last line of current 10min_currency_indices
unix_command = [ "tail -1" , " " , "/home/path/to/file" ] ;
[ ~ , data ] = system( unix_command ) ;
data = strsplit( data , ',' ) ; ## gives a cell arrayfun of characters
## zero pad singular month representations, i.e. 1 to 01
if ( numel( data{ 2 } == 1 ) )
data{ 2 } = [ '0' , data{ 2 } ] ;
endif
## and also zero pad singular dates
if ( numel( data{ 3 } == 1 ) )
data{ 3 } = [ '0' , data{ 3 } ] ;
endif
## and also zero pad singular hours
if ( numel( data{ 4 } == 1 ) )
data{ 4 } = [ '0' , data{ 4 } ] ;
endif
## and also zero pad singular minutes
if ( numel( data{ 5 } == 1 ) )
data{ 5 } = [ '0' , data{ 5 } ] ;
endif
## set up the headers
Hquery = [ 'curl -s -H "Content-Type: application/json"' ] ; ## -s is silent mode for Curl for no paging to terminal
Hquery = [ Hquery , ' -H "Authorization: Bearer XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX"' ] ;
query_begin = [ Hquery , ' "https://api-fxtrade.oanda.com/v3/instruments/' ] ;
## get time from last line of data
query_time = [ data{1} , '-' , data{2} , '-' , data{3} , 'T' , data{4} , '%3A' , data{5} , '%3A00.000000000Z&granularity=M10"' ] ;
## initialise with AUD_CAD
## construct the API call for particular cross
query = [ query_begin , iter_vec{ 1 } , '/candles?includeFirst=true&price=M&from=' , query_time ] ;
## call to use external Unix systems/Curl and return result
[ ~ , ret_JSON ] = system( query , RETURN_OUTPUT = 'TRUE' ) ;
## convert the returned JSON object to Octave structure
S = load_json( ret_JSON ) ;
## parse the returned structure S
if ( strcmp( fieldnames( S( 1 ) ) , 'errorMessage' ) == 0 ) ## no errorMessage in S
end_ix = numel( S.candles ) ; ## how many candles?
if ( S.candles{ end }.complete == 0 ) end_ix = end_ix - 1 ; endif ## account for incomplete candles
## create retval
retval = zeros( end_ix , 50 ) ; ## 45 currencies plus YYYY:MM:DD:HH:MM columns
for ii = 1 : end_ix
date_time = strsplit( S.candles{ ii }.time , { '-' , 'T' , ':' } ) ;
retval( ii , 1 ) = str2double( date_time( 1 , 1 ) ) ; ## year
retval( ii , 2 ) = str2double( date_time( 1 , 2 ) ) ; ## month
retval( ii , 3 ) = str2double( date_time( 1 , 3 ) ) ; ## day
retval( ii , 4 ) = str2double( date_time( 1 , 4 ) ) ; ## hour
retval( ii , 5 ) = str2double( date_time( 1 , 5 ) ) ; ## min
retval( ii , 6 ) = str2double( S.candles{ ii }.mid.c ) ; ## candle close price
endfor ## end of ii loop
else
error( 'Initialisation with AUD_CAD has failed.' ) ;
endif ## end of strcmp if
for ii = 2 : numel( iter_vec )
## construct the API call for particular cross
query = [ query_begin , iter_vec{ ii } , '/candles?includeFirst=true&price=M&from=' , query_time ] ;
## call to use external Unix systems/Curl and return result
[ ~ , ret_JSON ] = system( query , RETURN_OUTPUT = 'TRUE' ) ;
## convert the returned JSON object to Octave structure
S = load_json( ret_JSON ) ;
## parse the returned structure S
if ( strcmp( fieldnames( S( 1 ) ) , 'errorMessage' ) == 0 ) ## no errorMessage in S
end_ix = numel( S.candles ) ; ## how many candles?
if ( S.candles{ end }.complete == 0 ) end_ix = end_ix - 1 ; endif ## account for incomplete candles
temp_retval = zeros( end_ix , 6 ) ;
for jj = 1 : end_ix
date_time = strsplit( S.candles{ jj }.time , { '-' , 'T' , ':' } ) ;
temp_retval( jj , 1 ) = str2double( date_time( 1 , 1 ) ) ; ## year
temp_retval( jj , 2 ) = str2double( date_time( 1 , 2 ) ) ; ## month
temp_retval( jj , 3 ) = str2double( date_time( 1 , 3 ) ) ; ## day
temp_retval( jj , 4 ) = str2double( date_time( 1 , 4 ) ) ; ## hour
temp_retval( jj , 5 ) = str2double( date_time( 1 , 5 ) ) ; ## min
temp_retval( jj , 6 ) = str2double( S.candles{ jj }.mid.c ) ; ## candle close price
endfor ## end of jj loop
## checks dates and times allignment before writing to retval
date_time_diffs_1 = setdiff( retval( : , 1 : 5 ) , temp_retval( : , 1 : 5 ) , 'rows' ) ;
date_time_diffs_2 = setdiff( temp_retval( : , 1 : 5 ) , retval( : , 1 : 5 ) , 'rows' ) ;
if ( isempty( date_time_diffs_1 ) && isempty( date_time_diffs_2 ) )
## there are no differences between retval dates and temp_retval dates
retval( : , ii + 5 ) = temp_retval( : , 6 ) ;
elseif ( ~isempty( date_time_diffs_1 ) || ~isempty( date_time_diffs_2 ) )
## implies a difference between the date_times of retval and temp_retval, so merge them
dn_retval = datenum( [ retval(:,1) , retval(:,2) , retval(:,3) , retval(:,4) , retval(:,5) ] ) ;
dn_temp_retval = datenum( [ temp_retval(:,1) , temp_retval(:,2) , temp_retval(:,3) , temp_retval(:,4) , temp_retval(:,5) ] ) ;
new_dn = unique( [ dn_retval ; dn_temp_retval ] ) ; new_date_vec = datevec( new_dn ) ; new_date_vec( : , 6 ) = [] ;
new_retval = [ new_date_vec , zeros( size( new_date_vec , 1 ) , 45 ) ] ;
[ TF , S_IDX ] = ismember( new_retval( : , 1 : 5 ) , retval( : , 1 : 5 ) , 'rows' ) ;
TF_ix = find( TF ) ; new_retval( TF_ix , 6 : end ) = retval( : , 6 : end ) ;
[ TF , S_IDX ] = ismember( new_retval( : , 1 : 5 ) , temp_retval( : , 1 : 5 ) , 'rows' ) ;
TF_ix = find( TF ) ; new_retval( TF_ix , ii + 5 ) = temp_retval( : , 6 ) ;
retval = new_retval ;
clear new_retval new_dn dn_temp_retval dn_retval date_time_diffs_1 date_time_diffs_2 ;
else
error( 'Mismatch between dates and times for writing to retval.' ) ;
endif ## TF == S_IDX check
endif ## end of strcmp if
endfor ## ii loop
endfunction
This function is called in a script which uses the output matrix "retval" to then calculate the various currency strengths as outlined in the above linked posts. The total running time for this script is approximately 40 seconds from first call to appending to the index file on disk. I wrote this function to leverage my new found Oanda API knowledge to avoid having to accumulate an ever growing set of files on disk containing the raw 10 minute data.
I hope readers find this useful.
Tuesday, 7 February 2017
Update on Currency Strength Smoothing, and a new direction?
In the process of doing the above work I decided that my particle swarm routine wasn't fast enough and I started using the BayesOpt optimisation library, which is written in C++ and has an interface to Octave. Doing this has greatly decreased the time I've had to spend in my various optimisation routines and the framework provided by the BayesOpt library will enable more ambitious optimisations in the future.
Another discovery for me was this Predicting Stock Market Prices with Physical Laws paper, which has some really useful ideas for neural net input features. In particular I think the idea of combining position, velocity and acceleration with the ideas contained in an earlier post of mine on Savitzky Golay filter convolution and using the currency strength indicators as proxies for the arbitrary sine and cosine waves function posited in the paper hold some promise. More in due course.
Saturday, 3 September 2016
Possible Addition of NARX Network to Conditional Restricted Boltzmann Machine
- https://www.mathworks.com/help/nnet/ug/design-time-series-narx-feedback-neural-networks.html
- http://deeplearning.cs.cmu.edu/pdfs/Narx.pdf
- http://www.wseas.us/e-library/transactions/research/2008/27-464.pdf
- https://rucore.libraries.rutgers.edu/rutgers-lib/24889/
- https://arxiv.org/abs/1607.02093
- https://hal.archives-ouvertes.fr/hal-00501643/document
- http://www.theijes.com/papers/v3-i11/Version-1/C0311019026.pdf
- http://www.sciencedirect.com/science/article/pii/S0925231208003081
Friday, 5 February 2021
A Forex Pair Snapshot Chart
After yesterday's Heatmap Plot of Forex Temporal Clustering post I thought I would consolidate all the chart types I have recently created into one easy, snapshot overview type of chart. Below is a typical example of such a chart, this being today's 10 minute EUR_USD forex pair chart up to a few hours after the London session close (the red vertical line).
The top left chart is a Market/Volume Profile Chart with added rolling Value Area upper and lower bounds (the cyan, red and white lines) and also rolling Volume Weighted Average Price with upper and lower standard deviation lines (magenta).
The bottom left chart is the turning point heatmap chart as described in yesterday's post.
The two rightmost charts are also Market/Volume Profile charts, but of my Currency Strength Candlestick Charts based on my Currency Strength Indicator. The upper one is the base currency, i.e. EUR, and the lower is the quote currency.
The following charts are the same day's charts for:
GBP_USD,
USD_CHFand finally USD_JPYThe regularity of the turning points is easily seen in the lower lefthand charts although, of course, this is to be expected as they all share the USD as a common currency. However, there are also subtle differences to be seen in the "shadows" of the lighter areas.For the nearest future my self-assigned task will be to observe the forex pairs, in real time, through the prism of the above style of chart and do some mental paper trading, and perhaps some really small size, discretionary live trading, in additional to my normal routine of research and development.
Thursday, 7 June 2018
Update on Improved Currency Strength Indicator
% aud_cad
mse_vector(1) = log( ( current_data(1,1) * ( aud_x / cad_x ) ) / current_data(2,1) )^2 ;
% xau_aud
mse_vector(46) = log( ( current_data(1,46) * ( gold_x / aud_x ) ) / current_data(2,46) )^2 ;
% xau_cad
mse_vector(47) = log( ( current_data(1,47) * ( gold_x / cad_x ) ) / current_data(2,47) )^2 ;which shows the optimisation errors for the "old" way of doing things, in black, and the revised way in blue. Note that this is a log scale, so the errors for the revised way are orders of magnitude smaller, implying a better model fit to the data.
This next chart shows the difference between the two methods of calculating a gold index ( black is old, blue is new ),
this one shows the calculated USD index
and this one the GBP index in blue, USD in green and the forex pair cross rate in black
The idea(s) I am going to look at next is using these various calculated indices as inputs to algorithms/trading decisions.