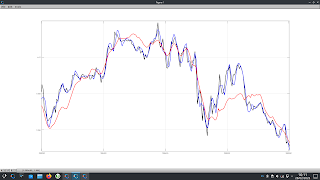
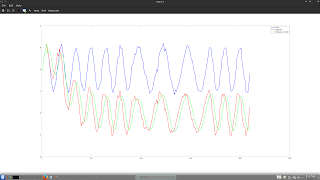
During the course of writing this blog I have visited the idea of using Kalman filters several times, most recently in this February 2023 post. My motivation in these previous posts could best be described as trying to smooth price data with as little lag as possible, i.e. create a zero-lag indicator. In doing so, the model most often used for the Kalman filter was a physical motion model with position, velocity and acceleration components. Whilst these "worked" in the sense of smoothing the underlying data, it is not necessarily a good model to use on financial data because, obviously, financial data is not a physical system and so I thought I would apply the Kalman filter to something that is ubiquitously used on financial data - the Exponential moving average.
Below is an Octave function to calculate a "Kalman_ema" where the prediction part of the filter is just a linear extrapolation of an exponential moving average and then this extrapolated value is used to calculate the projected price, with the measurement being the real price and its ema value.
## Copyright (C) 2024 dekalog
##
## This program is free software: you can redistribute it and/or modify
## it under the terms of the GNU General Public License as published by
## the Free Software Foundation, either version 3 of the License, or
## (at your option) any later version.
##
## This program is distributed in the hope that it will be useful,
## but WITHOUT ANY WARRANTY; without even the implied warranty of
## MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
## GNU General Public License for more details.
##
## You should have received a copy of the GNU General Public License
## along with this program. If not, see .
## -*- texinfo -*-
## @deftypefn {} {@var{retval} =} kalman_ema (@var{price}, @var{lookback})
##
## @seealso{}
## @end deftypefn
## Author: dekalog
## Created: 2024-04-08
function [ filter_out , P_out ] = kalman_ema ( price , lookback )
## check price is row vector
if ( size( price , 1 ) > 1 && size( price , 2 ) == 1 )
price = price' ;
endif
P_out = zeros( numel( price ) , 2 ) ;
ema_price = ema( price , lookback )' ;
alpha = 2 / ( lookback + 1 ) ;
## initial covariance matrix
P = eye( 3 ) ;
## transistion matrix
A = [ 0 , ( 1 + alpha ) / alpha , -( 1 / alpha ) ; ...
0 , 2 , -1 ; ...
0 , 1 , 0 ] ;
## initial Q
Q = eye( 3 ) ;
## measurement vector
Y = [ price ; ...
ema_price ; ...
shift( ema_price , 1 ) ] ;
Y( 3 , 1 ) = Y( 2 , 1 ) ;
## measurement matrix
H = eye( 3 ) ;
## measurement noise covariance
R = eye( 3 ) ;
## container for Kalman filter output
filter_out = zeros( size( Y ) ) ;
errors = ones( 3 , 1 ) ;
for ii = 2 : size( Y , 2 )
X = A * filter_out( : , ii - 1 ) ;
P = A * P * A' + Q ;
errors = alpha .* abs( X - Y( : , ii ) ) + ( 1 - alpha ) .* errors ;
IM = H * X ; ## Mean of predictive distribution
IS = ( R + H * P * H' ) ; ## Covariance of predictive mean
K = P * H' / IS ; ## Computed Kalman gain
X = X + K * ( Y( : , ii ) - IM ) ; ## Updated state mean
P = P - K * IS * K' ; ## Updated state covariance
filter_out( : , ii ) = X ;
P_out( ii , 1 ) = P( 1 , 1 ) ;
P_out( ii , 2 ) = P( 2 , 2 ) ;
## update Q and R
Q( 1 , 1 ) = errors( 1 ) ; Q( 2 , 2 ) = errors( 2 ) ; Q( 3 , 3 ) = errors( 3 ) ;
R = Q ;
endfor
filter_out = filter_out' ;
endfunction 
Despite the wide range of the input look back lengths for the ema, it can be seen that the covariance bands around price are broadly similar. I can think of many uses for such a data driven but basically parameter insensitive measure of price variance, e.g. entry/exit levels, stop levels, position sizing etc.
More in due course.
