## Copyright (C) 2018 dekalog
##
## This program is free software; you can redistribute it and/or modify it
## under the terms of the GNU General Public License as published by
## the Free Software Foundation; either version 3 of the License, or
## (at your option) any later version.
##
## This program is distributed in the hope that it will be useful,
## but WITHOUT ANY WARRANTY; without even the implied warranty of
## MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
## GNU General Public License for more details.
##
## You should have received a copy of the GNU General Public License
## along with this program. If not, see .
## -*- texinfo -*-
## @deftypefn {} {@var{spread}, @var{spread_0 =} bid_ask_spread (@var{high}, @var{low}, @var{close})
##
## This function takes vectors of observed high, low and close prices and calculates
## the closed form bid-ask spread, as outlined in
##
## "A Simple Way to Estimate Bid-Ask Spreads from Daily High and Low Prices"
## ( Corwin and Schultz, 2012 )
##
## The first output is the bid-ask spread with zero values interpolated by use
## of an Exponential moving average (default value of 20 bars) whilst the
## second output is the bid-ask spread without this interpolation, and hence
## possibly contains zero values.
##
## Paper available at https://www3.nd.edu/~scorwin/
##
## @seealso{}
## @end deftypefn
## Author: dekalog
## Created: 2018-12-11
function [ spread2 , spread ] = bid_ask_spread ( high , low , close )
hilo_ratio_1 = high ./ low ;
hilo_ratio_2 = max( [ high shift( high , 1 ) ] , [] , 2 ) ./ min( [ low shift( low , 1 ) ] , [] , 2 ) ;
% adjust for overnight price gaps
% gap up
close_shift = shift( close , 1 ) ; close_shift( 1 ) = low( 1 ) ;
ix = find( low > close_shift ) ;
if ( ~isempty( ix ) )
estimated_overnight_price_increases = low( ix ) .- close( ix .- 1 ) ;
hilo_ratio_1( ix ) = ( high( ix ) .- estimated_overnight_price_increases ) ./ ( low( ix ) .- estimated_overnight_price_increases ) ;
hilo_ratio_2( ix ) = max( [ ( high( ix ) .- estimated_overnight_price_increases ) high( ix .- 1) ] , [] , 2 ) ...
./ min( [ ( low( ix ) .- estimated_overnight_price_increases ) low( ix .- 1 ) ] , [] , 2 ) ;
endif
% gap down
close_shift( 1 ) = high( 1 ) ;
clear ix ;
ix = find( high < close_shift ) ;
if ( ~isempty( ix ) )
estimated_overnight_price_decreases = close( ix .- 1 ) .- high( ix ) ;
hilo_ratio_1( ix ) = ( high( ix ) .+ estimated_overnight_price_decreases ) ./ ( low( ix ) .+ estimated_overnight_price_decreases ) ;
hilo_ratio_2( ix ) = max( [ ( high( ix ) .+ estimated_overnight_price_decreases ) high( ix .- 1) ] , [] , 2 ) ...
./ min( [ ( low( ix ) .+ estimated_overnight_price_decreases ) low( ix .- 1 ) ] , [] , 2 ) ;
endif
beta = log( hilo_ratio_1 ) .^ 2 ; beta = beta .+ shift( beta , 1 ) ;
gamma = log( hilo_ratio_2 ) .^ 2 ;
alpha = ( sqrt( 2 .* beta ) .- sqrt( beta ) ) ./ ( 3 .- 2 .* sqrt( 2 ) ) .- sqrt( gamma ./ ( 3 .- 2 .* sqrt( 2 ) ) ) ;
spread = exp( alpha ) ; spread = 2 .* ( spread .- 1 ) ./ ( 1 .+ spread ) ;
spread( 1 ) = spread( 2 ) ; spread( spread < 0 ) = 0 ;
ndays = 20 ;
ema_alpha = 2 / ( ndays + 1 ) ;
avg = filter( ema_alpha , [ 1 ema_alpha - 1 ] , spread , spread(1) ) ;
clear ix ;
spread2 = spread ;
ix = find( spread == 0 ) ; spread2( ix ) = avg( ix ) ;
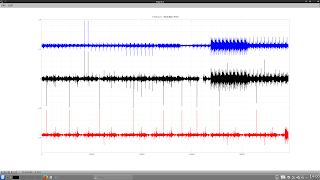
endfunction the black line is an interpolated spread using an exponential moving average where the raw spread calculations are zero (this is my own addition) and the red line is the spread without interpolation. Note: the y-axis is expressed as percentage values.
The reasons why one might use this function are outlined in the above linked paper. Enjoy!